We recently became fans of an annotation methodology called Best-worst scaling developed by Jordan Louviere (University of Alberta) in 1987, and its application to linguistic annotation as proposed by Svetlana Kiritchenko and Saif M. Mohammad at the National Research Council Canada. In a nutshell, the method involves asking the annotators to select the most and least relevant items off a tuple of instances with respect to the phonomenon under study. This is in contrast to the usual annotation procedures, where items are typically presented to the annotator one by one, and this variant has shown to lead to an easier annotation procedure, which in turn yields more reliable results.

For a simple example, imagine we want to annotate sentiment polarity: a natural language message has to be judged as whether containing a positive or negative (or neutral) sentiment. Usual methods require a group of annotators (perhaps in a crowdsourcing setting) reading through the list of messages and judging them either by a strict classification (e.g. positive/neutral/negative), a non-exclusive set of labels (like in SENTIPOLC), a value on a continuous scale, or anything else. With BWS, we instead present the annotator tuples of (for instance) 4 elements A, B, C, D, and ask them two questions: “which message among A, B, C, and D expresses the most positive sentiment?” and “which message among A, B, C, and D expresses the most negative sentiment?”. Of course, this scheme can be applied to any other target phenomenon that could be modeled on a latent scale.

In practice, BWS needs a little preprocessing to be used. In particular, the tuples need to be created starting from the original set of instances to annotate, and they should follow some specific contraints. First, we need to decide a fixed size for the tuples, let’s call that k. Then, each instance has to appear in exactly the same number of tuples (let’s call this number p). Finally, no pair of instances can appear in more than one tuple.

Given these constraints and a set of numbered instances (e.g., messages to annotate with sentiment polarity), how do we generate the tuples? An easy solution could be to generate random subsets of K elements and adding them to the final set of tuples if they obey the constraints above. Besides being computationally inefficient (and perhaps not the most elegant, although that’s debatable), this method has a problem. It works if we have an abundant source of unannotated instances and we are only interested in annotating some of them, but otherwise it is tricky to put all the instances in tuples for BWS this way.

Can we do better? My friend Marco from ACMOS asked me this question (sort of), and I ended up spending a whole weekend (and, admittedly, having a lot of nerdy fun) on what turned out to be a nice little combinatorial puzzle. The basic idea uses Gauss’ modular arithmetic to evenly distribute the original instances in a way that satisfy the three constraints. It has to be parametric too, in order to account for the varying number and size of the tuples. This is what I ended up with.

For n instances, there will be n/k tuples times p. Therefore, with x ranging between 0 and n/k, and j ranging between 0 and k, each tuple is composed by the instances identified by the formula:

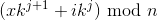
Where i ranges between 0 and k.

It sounds a bit complicated, but it makes sense once looking at the output. Let’s try with a set of 101 instances, asking for 4-uples with each instance repeating in exactly 4 4-uples (k=4, p=4). The first tuples we get are

1, 2, 3, 4
5, 6, 7, 8
...

and so on. Then, once we get to n (101), the formula starts to wrap the indexes around:

...
1, 5, 9, 13
81, 85, 89, 93
97, 101, 4, 8
12, 16, 20, 24
...

Nice, huh? It comes with a couple of caveats though. First, n (the number of instances) and k (the size of the tuples) must be co-primes, i.e., they need not have common divisors other than 1. The other issue is that although we can produce an almost perfect set of tuples given the initial instances, it is mathematically impossible to have all the instances appear in exactly p tuples. More precisely, there will be up to k-1 instances that occur p-1 times. In other words, a very small set of instances will lack one annotation.

I wrote a simple Python script to test this idea and put it on Github along with an example dataset. I look forward to get some feedback, and especially to be corrected about the statements in the last paragraph!